5 Extremes of Stationary Processes
Here, we will explore the impact of dependence between values in the series on the extreme values when observed at long-range and short-range. As previously we will focus on
- \(M_n=\max(X_1, \ldots ,X_n)\);
- exceedances of a high threshold.
5.1 Background
A process \(\{X_t\}\) is said to be a stationary process if the joint distributions of \[\begin{eqnarray*} (X_{t_1}, \ldots ,X_{t_k})\mbox{ and } (X_{t_1+\tau}, \ldots ,X_{t_k+\tau}) \end{eqnarray*}\] are the same for any \(k\), \(t_1, \ldots ,t_k\) and \(\tau\). Throughout we will assume that the univariate marginal distribution function is \(F\), i.e. \[\begin{eqnarray*} F(x)=\Pr(X_t\leq x) \mbox{ for all }t. \end{eqnarray*}\]
5.1.1 Long-range asymptotic independence condition
We suppose that there exist normalising sequences \(a_{n}\) and \(b_{n}\) such that \[\begin{eqnarray*} \frac{M_{n} - b_{n}}{a_{n}} \end{eqnarray*}\] has a non-degenerate limit distribution. We want to characterise the limit behaviour of this variable. In the absence of any conditions that limit the amount of long-range dependence that can be present in the values of the series, any limit distribution can be obtained.
For example let \(X_t=X_1\) for all \(t\), then for all \(n\) \[\begin{eqnarray*} \Pr(M_n\leq x)=\Pr(X_1\leq x)=F(x), \end{eqnarray*}\] so the class of limit distributions covers all distributions.
Again, let’s see what we can learn from the CLT. A CLT for stationary processes exists and this also has to limit long-range dependence. The condition is termed strong mixing, it ensures that events separated sufficiently in time are effectively independent and so allows there to be enough independent variables for a CLT on these variables to apply.
5.1.2 Asymptotic independence of Maxima (AIM)
Let \(M_{i,j}=\max(X_i, \ldots, X_j)\) and \(u_{n} = a_{n} x + b_{n}\) for \(a_n, b_n\) defined above and \(x\) any real number.
The AIM\((u_n)\) condition is that there exists a sequence \(q_{n}\) of positive integers with \(q_{n} = o(n)\) such that for all \(i\) and \(j\) \[\begin{align} \max |&\Pr (M_{1,i} \leq u_{n} , M_{i+q_{n}, i+q_{n}+j } \leq u_{n}) - \nonumber\\ &\Pr (M_{1,i} \leq u_{n}) \Pr (M_{1,j} \leq u_{n}) | \rightarrow 0\mbox{ as }n \rightarrow \infty. \label{eq:AIM} \end{align}\]
The condition ensures that separated groups of extreme points become increasingly close to being independent as their separation and level both increase at appropriate rates.
There are many other similar conditions depending on the particular extremal property that is of interest, see Leadbetter, Lindgren, and Rootzén (1983) and O’Brien (1987).
5.2 Unified Extremal Types Theorem for stationary sequences
Theorem Suppose that there exist normalising sequences \(a_{n}\) and \(b_{n}\) such that \[\begin{eqnarray*} \Pr\left(\frac{M_{n} - b_{n}}{a_{n}}\leq x\right) \rightarrow H(x) \mbox{ as } n\rightarrow \infty, \end{eqnarray*}\] where \(H\) is a non-degenerate distribution, and that the AIM\((a_n x+b_n)\) condition holds, then \(H\) is of the same type as \[\begin{eqnarray*} \exp\left[-(1+\xi x)_+^{-1/\xi}\right], \end{eqnarray*}\] i.e. a GEV limit distribution.
Outline strategy of proof
- partition time into a series of alternating long and short blocks, \(k\) of each;
- let the numbers in long and short blocks be \(r_n\) and \(q_n\) respectively with \(r_n\rightarrow \infty\), \(q_n\rightarrow \infty\) and \(q_n/r_n\rightarrow 0;\)
- in a neighbouring pair of long and short blocks, the maximum over the two blocks is likely to be in the long block;
- all maxima tend to fall into the long blocks;
- long block maxima are approximately independent as they are separated in time by the short blocks, so satisfy AIM\((u_n)\) condition;
- long block maxima satisfy the max-stability property, and hence are GEV.
A few comments on this theorem:
- at a practical level this is all we need, the maximum of a stationary sequence that has some independence at long-range follows a GEV distribution;
- the result does not show how the dependence changes the behaviour of \(M_n\);
We separate marginal and dependence features for the remainder of the chapter and subsequently fix the marginal distribution \(F\) of the \(\{X_t\}\) to be Fréchet.
5.2.1 Extremes of Fréchet marginal variables
Let \(\{X_t\}\) be a stationary process which has Fréchet marginal distributions, i.e. \[\begin{eqnarray*} F(x)=\exp(-1/x)\mbox{ for }x>0. \end{eqnarray*}\] Let \(\hat{M}_n\) denote the maximum of \(n\) IID variables with marginal distribution \(F\) then \[\begin{eqnarray*} \Pr\left(\frac{\hat{M}_n}{n}\leq x\right)=\{F(nx)\}^n=\exp(-1/x)=G(x), \end{eqnarray*}\] i.e. \(\hat{M}_n/n\) has a Fréchet limit distribution for all \(n\) and we denote the limit distribution of the maximum of the IID variables by \(G\).
Suppose that \(M_n=\max(X_1, \ldots ,X_n)\), that \(\{X_t\}\) satisfies the AIM\((nx)\) condition and that \[\begin{eqnarray*} \Pr\left(\frac{M_n}{n}\leq x\right)\rightarrow H(x), \end{eqnarray*}\] then we can assess the effect of dependence on \(M_n\) by looking at the difference between \(H\) and \(G\).
5.2.2 Motivating Example: Moving Maxima
Let \(\{Y_t\}\) be IID with \(F_Y(y)=\exp[-1/(2y)]\), i.e. Fréchet type marginals. Define, for all \(t\) \[\begin{eqnarray*} X_t=\max(Y_t,Y_{t-1}) \end{eqnarray*}\] An example of this process is shown in Figure 5.1.
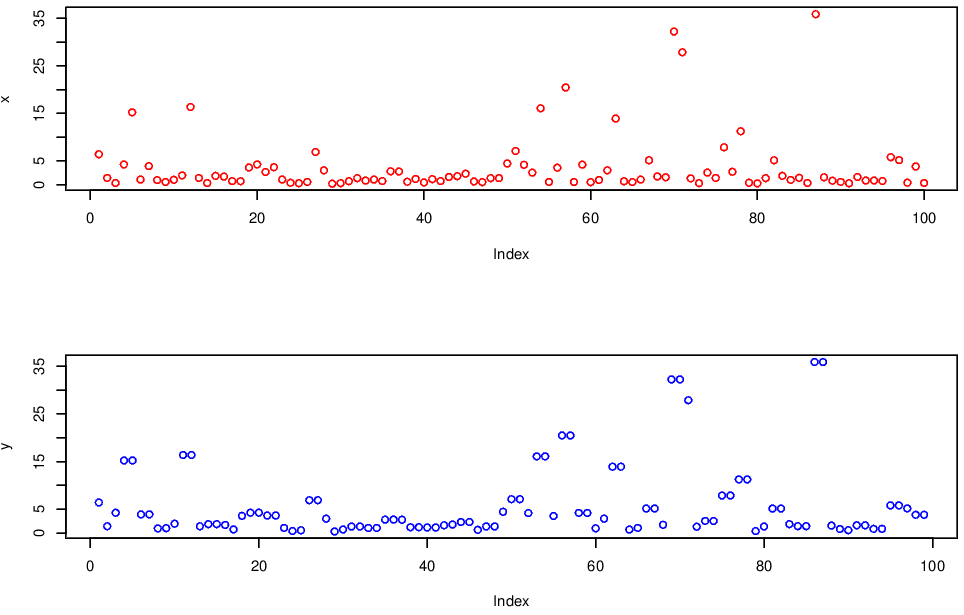
Figure 5.1: Example of a moving maxima process.
Marginal properties
The marginal distribution of the \(\{X_t\}\) process is:
\[\begin{eqnarray*}
\Pr(X_t\leq x) & = & \Pr(Y_t\leq x,Y_{t-1}\leq x)\\
& = & \{F_Y(x)\}^2\\
& = & \exp[-2/(2x)]\\
& = & \exp(-1/x),
\end{eqnarray*}\]
i.e. Fréchet distributed.
Dependence properties
- For \(\tau>1\), \((X_t,X_{t+\tau})\) is independent as the associated \(Y\) variables are all different for each of the \(X\)’s and hence the \(X\)’s are independent.
- For \(\tau=1\), \((X_t,X_{t+\tau})\) is dependent as the both \(X_t\) and \(X_{t+1}\) are functions of \(Y_t\);
- it is clear that long-range independence holds;
- extreme values occur as groups or clusters of independent values, with two values per cluster for all the largest values.
Derivation of \(H\) \[\begin{eqnarray*} \Pr\left(\frac{M_n}{n}\leq x\right) & = & \Pr(X_1\leq nx, \ldots ,X_n \leq nx)\\ & = & \Pr(Y_0\leq nx, Y_1\leq nx, \ldots ,Y_n\leq nx)\\ & = & [F_Y(nx)]^{n+1}\\ & = & \{\exp[-1/(2nx)]\}^{n+1}\\ & = & \exp[-(n+1)/(2nx)]\\ & \rightarrow & \exp[-1/(2x)]\mbox{ as }n\rightarrow \infty\\ & = & \{G(x)\}^{1/2}\\ & = & H(x). \end{eqnarray*}\]
5.3 The Extremal Index
The previous example shows that short-range dependence in the extreme values of the process affects the limiting distribution of \(M_n\). Before expanding on this further, we first present a measure of short-range extremal dependence, termed the extremal index.
Define the extremal index \(\theta\), for variables with Fréchet marginals, by \[\begin{eqnarray*} \theta & = & \lim_{n\rightarrow \infty} \Pr(M_{2,p_n}\leq n\,|\, X_1>n)\\ & =& \lim_{n\rightarrow \infty} \{1-\Pr(M_{2,p_n}> n\,|\, X_1>n)\} \end{eqnarray*}\] where \(p_n=o(n)\).
The extremal index has the following features:
- \(0\le \theta \leq 1\);
- larger values of \(\theta\) correspond to weaker short-range extremal dependence;
- for an IID process \(\theta=1\) as \[\begin{eqnarray*} \theta & = & \lim_{n\rightarrow \infty} \{F(n)\}^{p_n}\\ & = & \lim_{n\rightarrow \infty} \exp(-p_n/n)\\ & \rightarrow & 1 \mbox{ as }n\rightarrow \infty, \end{eqnarray*}\] (since \(p_n/n\rightarrow 0\));
- if a process is independent for all lags \(\tau\ge m\), for some finite \(m\) then \(1/m\le \theta \le 1\).
5.3.1 Extremal index for Moving Maxima example
From the realisation of the process it is clear that \(\theta=1/2\). The theoretical derivation is \[\begin{eqnarray*} \Pr(M_{2,p_n}\leq n\,|\, X_1>n) & = & \Pr(Y_1\leq n, Y_2\leq n,\ldots ,Y_{p_n}\leq n\,|\, \max(Y_0,Y_1)>n)\\ & \approx & \Pr(Y_1\leq n, Y_2\leq n,\ldots ,Y_{p_n}\leq n\,|\, Y_0>n)\times\frac{1}{2}\\ & & + \Pr(Y_1\leq n, Y_2\leq n,\ldots ,Y_{p_n}\leq n\,|\, Y_1>n)\times\frac{1}{2}\\ & \rightarrow & 1\times \frac{1}{2}+0\times \frac{1}{2}\\ & = & \frac{1}{2}=\theta. \end{eqnarray*}\]
5.3.2 Implications of short-range extremal dependence
Combining the above results and examples, the following result should appear to be quite natural.
For variables with Fréchet marginal distributions, provided that \(\Pr(M_n/n\leq x)\rightarrow H(x)\) as \(n\rightarrow \infty\) to a non-degenerate limit \(H\) then if
- AIM\((nx)\) condition holds;
- \(\theta\) exists
then \[\begin{eqnarray*} H(x)=\{G(x)\}^{\theta}. \end{eqnarray*}\]
The implications of this result are that, except for a really weak long-range dependence condition:
- for stationary processes the effect of dependence is through \(\theta\) only;
- \(\theta\) can be absorbed into the normalising constants, so dependence does not change the limiting type;
- the limit suggests \[\begin{eqnarray*} H(x)=\lim_{n\rightarrow \infty}\left[\{F(nx)\}^n\right]^{\theta} =\lim_{n\rightarrow \infty}\{F(nx)\}^{n\theta}, \end{eqnarray*}\] so \(n\theta\) can be thought of as an effective number of independent variables.
5.3.3 Distribution of the Maximum
Consider random variables \(X_1, \ldots ,X_n\) with arbitrary distribution function \(F\) and which satisfy the AIM\((u_n)\) condition. As \(n\rightarrow \infty\) \[\begin{eqnarray*} \Pr\left(\frac{M_n-b_n}{a_n}\leq y\right) \rightarrow \exp\left[-\theta \left\{1+\xi\left(\frac{y-\mu}{\sigma}\right)\right\}_+^{-1/\xi}\right], \end{eqnarray*}\] where if the variables are IID \(\theta=1\).
5.3.4 Threshold exceedances
We assume that
- \(\{X_t\}\) is a stationary process with arbitrary distribution function \(F\);
- the required norming constants for an IID process with marginal \(F\) are \(a_n\) and \(b_n\) with limit distribution \(G\), a GEV\((0,1,\xi)\) distribution;
- a long-range asymptotic independence condition (similar to the AIM\((a_nx+b_n)\) condition) holds.
Consider the point processes \[\begin{eqnarray*} P_n=\left\{\left(\frac{i}{n+1},\frac{X_i-b_n}{a_n}\right);i=1, \ldots ,n\right\} \end{eqnarray*}\] on \([0,1]\times [0,\infty)\). Figure 5.2 shows a point process \(P_n\) for \(n=10,100,1000,10000\) respectively with \[ X_t = \max(\alpha_0Y_t,~\alpha_1Y_{t-1},~\alpha_2Y_{t-2}), \] where \(\{Y_t\}\) is an IID process as before, and \(\alpha_0=\frac{1}{3}\), \(\alpha_1=\frac{1}{2}\), and \(\alpha_2=\frac{1}{6}\). Equivalently, we say \(X_t\sim\) Moving Max \(\left(\alpha_0=\frac{1}{3},\alpha_1=\frac{1}{2},\alpha_2=\frac{1}{6}\right)\).
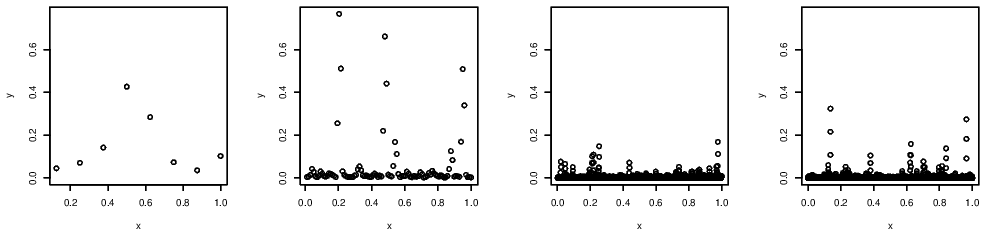
Figure 5.2: Point process \(P_n\) representation of the moving maxima process for \(n=10,100,1000,10000\).
5.3.5 Cluster maxima point process intensity
For data over a high threshold \(u\) we absorb the location and scale normalisation into the parameters to give the intensity of the non-homogeneous Poisson Process for the cluster maxima as \[\begin{eqnarray} \lambda(t,y)=\theta \sigma^{-1}[1+\xi (y-\mu)/\sigma]_+^{-1-1/\xi} \label{eqn:clust.max.intensity} \end{eqnarray}\]
Implications of the limit process: clusters
Fixing a threshold level \(u>b_l\) we have that:
- clusters are those set of points exceeding \(u\) which occur at the same normalised time. In the original series these are large points which occur within a short time period of one another.
- the expected number of exceedances of \(u\) per cluster (for which the cluster maxima exceeds \(u\)) is \(\theta^{-1}\), irrespective of the level \(u\);
- relative to independent series, when \(\theta<1\) there are fewer clusters (by a factor \(\theta\)) and more exceedances per cluster (by a factor \(\theta^{-1}\));
- values in one cluster are independent of values in another cluster;
- values within a cluster are dependent.
Implications of the limit process: exceedances
Fixing a threshold level \(u>b_l\) we have that:
- the rate of cluster maxima exceeding the threshold \(u\) is \[\begin{eqnarray*} \theta [1+\xi(u-\mu)/\sigma]_+^{-1/\xi}. \end{eqnarray*}\]
- the rate of arbitrary values exceeding the threshold \(u\) is \[\begin{eqnarray*} [1+\xi(u-\mu)/\sigma]_+^{-1/\xi}. \end{eqnarray*}\]
- the cluster maxima that exceed the threshold are independent, and follow a GPD\((\sigma_u,\xi)\), with shape parameter \(\xi\); GPD\((\sigma_u,\xi)\) model for cluster maxima excesses over \(u\), where \[\begin{eqnarray*} \sigma_u=\sigma+\xi(u-\mu). \end{eqnarray*}\]
- arbitrary (in time) excesses over \(u\) also follow a GPD\((\sigma_u,\xi)\), i.e. with the same parameters as the cluster maxima;